CVPR 2022 Oral | 回归标签不平衡? 试试Balanced MSE

标签的不平衡是现实世界中视觉回归里常见的问题，例如在年龄回归问题中，可能大部分训练样本都来自于成年人，老人与儿童的训练样本则相对较少。常用的Mean Square Error (MSE) 损失函数在少见样本上的表现往往不尽如人意，因此越来越多的研究开始重视不平衡回归，大规模评测集也在最近被提出[1]。相比于已经被广泛研究的不平衡分类，针对不平衡回归的研究工作相对较少。较早的研究试图通过生成的方法来增加少见标签的训练样本[2]，但样本生成在面对图像等高维数据时可行性较低。最近的研究主要采用重加权来提高少见标签在训练集中的权重[1]，但重加权在不平衡分类中已被证明效果有限[3]，我们也通过实验在不平衡回归上验证了这一点。因此，不平衡回归问题还处于一个起步阶段，目前依然缺少行之有效的方法。

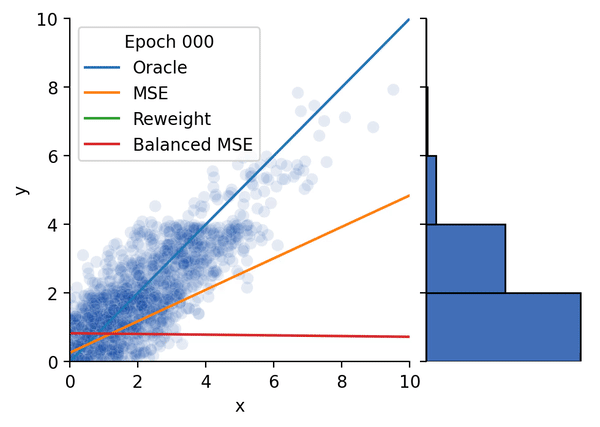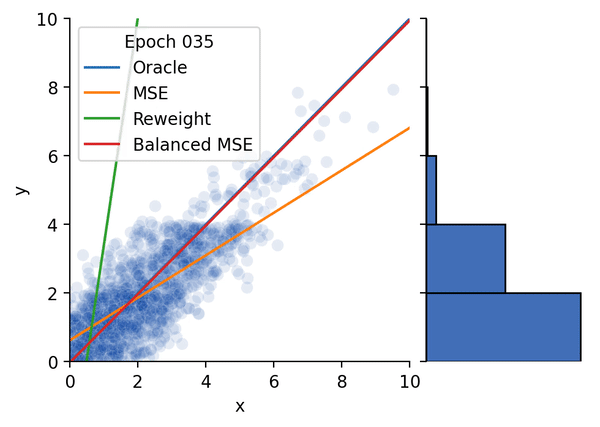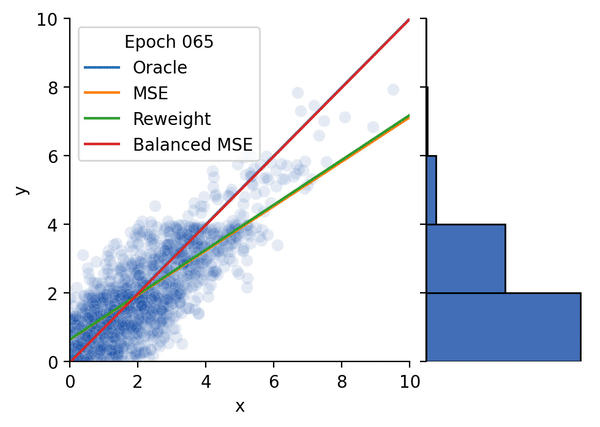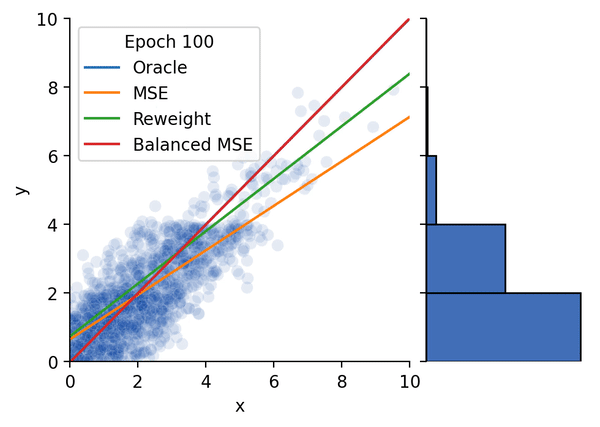
图1 不平衡回归示例

为了填补不平衡回归方法的空白，我们提出了Balanced MSE损失函数，从统计的视角解决标签的不平衡。

1. 重新思考MSE损失函数

我们首先重新审视了常用的MSE损失函数，发现当训练数据不平衡时，MSE会被标签分布所影响而倾向于预测常见的标签。当测试集是平衡的或衡量指标是平衡的时候，MSE的这一特点会导致模型在整体标签上的平均表现变差。我们沿着这个思路，使用概率的方法摆脱了不平衡的标签分布对MSE的影响。我们将改进后的损失函数称作Balanced MSE。

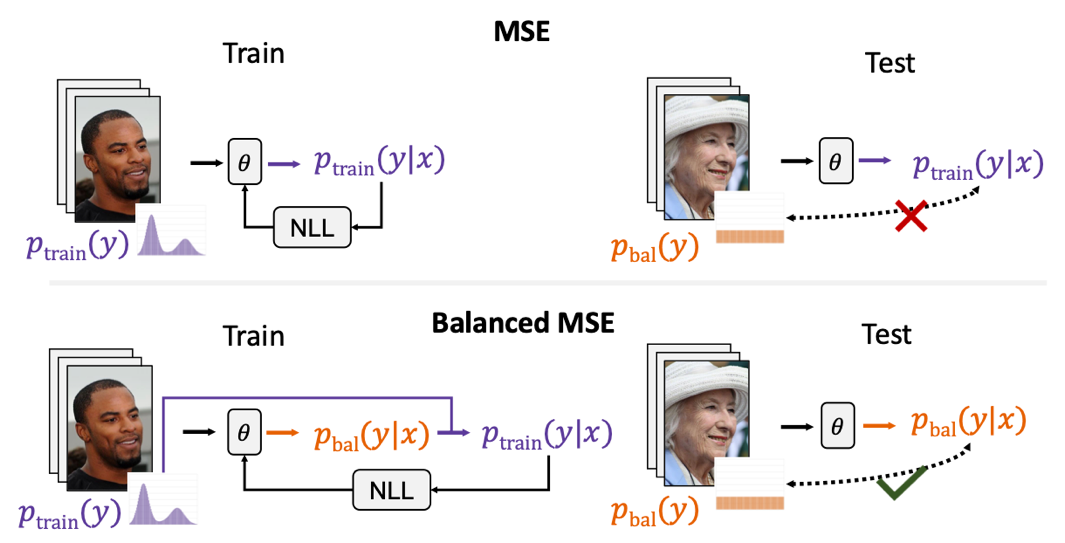
图2 统计视角下的MSE与Balanced MSE

2. 统一视角下的不平衡分类与回归

其实从统计的视角解决标签不平衡的思路在不平衡分类中也被深入讨论过，其中我们在NeurIPS 2020的工作Balanced Softmax [4]在长尾视觉分类上带来了显著的性能提升。然而由于MSE损失函数的概率意义很少被提及，这个思路在不平衡回归问题上是首次被探讨。不仅如此，我们也通过我们的两篇工作，Balanced Softmax与Balanced MSE，第一次将不平衡分类与不平衡回归融入了统一的框架中讨论。未来更多的不平衡分类技巧也可通过这个框架被引入不平衡回归的领域中。

3. 灵活的实现

我们为Balanced MSE中关于标签分布的积分计算提供了灵活的实现方式。我们提出的实现中既可以使用传统的分段标签分布，也可以使用使用高斯混合模型拟合的标签分布，甚至可以不依赖任何预先处理的标签分布。这里我们着重介绍不依赖预处理标签分布的实现方式，我们称为BMC。BMC从每个训练batch中估计标签分布信息，因此不需要进行任何额外的操作即可替换常用的MSE损失函数。BMC的形式也十分有趣，可以等价于将训练batch中对每个标签看作类别进行分类。其中，分类的logit由标签与预测之间的L2距离获得，非常类似自监督学习中使用的contrastive loss。得益于此，BMC可以简单地通过分类中的的交叉熵损失函数快速实现。

图3 Balanced MSE的BMC形式不依赖标签分布，可以通过几行代码快速实现

我们在首先使用合成数据集对Balanced MSE进行了实验。图4 展示了Balanced MSE在不同的标签分布下都能得到最接近真实线性关系的结果，而重加权方法的表现则随着标签分布越来越不平衡变得越来越差。

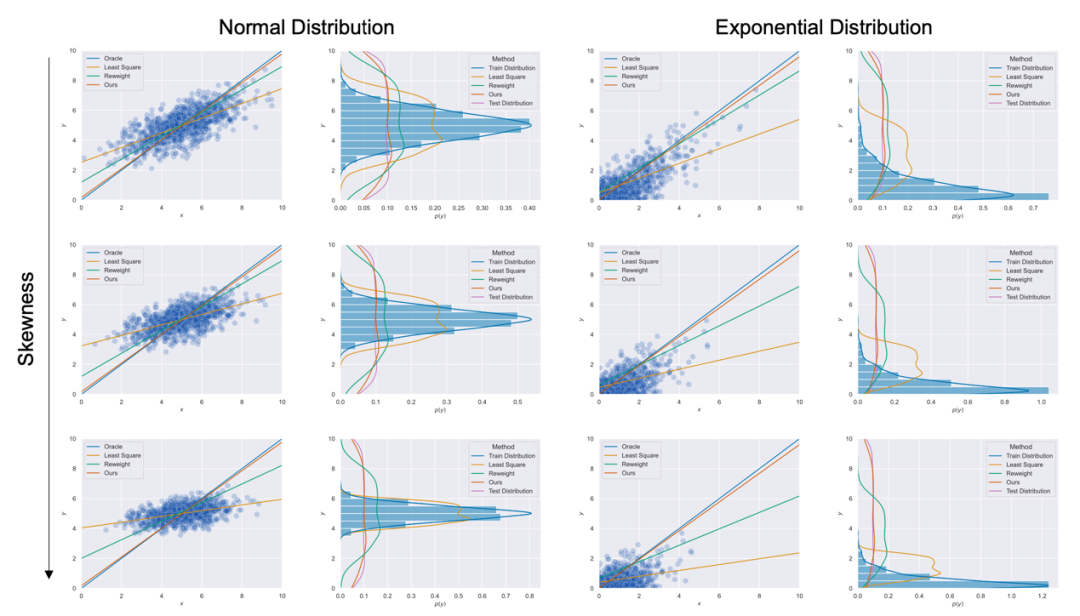
图4 Balanced MSE在不同标签分布下的一维不平衡回归

图5和图6分别展示了Balanced MSE在多维不平衡回归与非线性不平衡回归中依然能取得当前最好的表现。

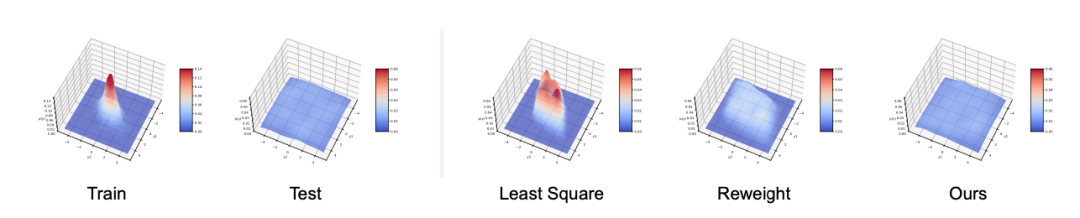
图5 Balanced MSE适用于多维不平衡回归

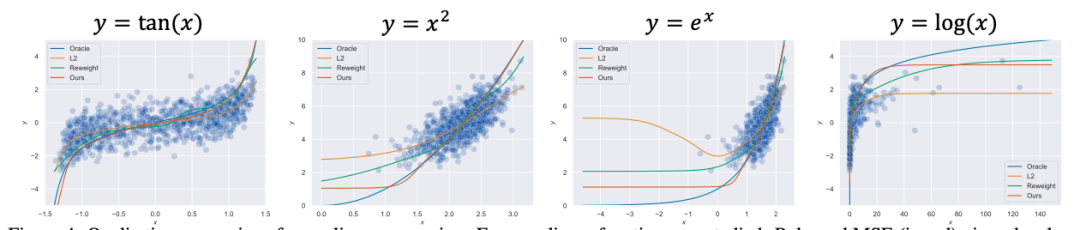
图6 Balanced MSE适用于一维非线性回归

除此之外，我们在三个真实数据集上验证了Balanced MSE的效果，其中包括包含两个一维不平衡回归问题：年龄回归与深度回归，以及一个我们提出的多维不平衡回归问题：人体mesh估计[5]。我们的方法均显著超过了当前的最优算法。图7中可以看到Balanced MSE显著提升了对儿童和老人等少数群体的年龄估计表现。图8显示Balanced MSE可以有效估计少见的姿态，能够帮助恢复出完整的动作幅度。

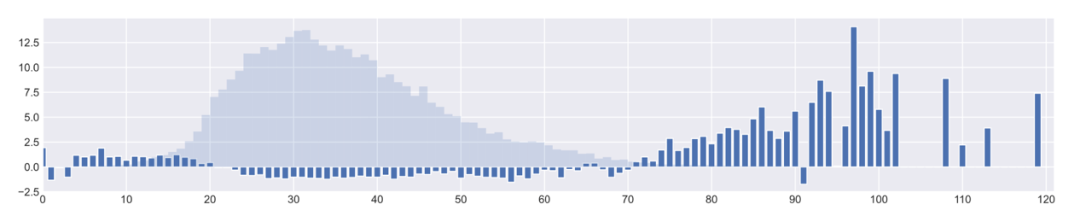
图7 Balanced MSE在不平衡年龄回归数据集上取得的表现提升

图8 在人体mesh估计上表现对比，左边为基线，右边为Balanced MSE

我们针对不平衡回归的问题设定，从统计的视角下重新思考了常用的MSE损失函数，发现MSE会受到不平衡标签分布的影响而做出不准确的预测。为解决这个问题，我们提出了Balanced MSE损失函数，并给出了灵活的实现形式，包括不需要预先计算标签分布的实现。Balanced MSE在一维与多维的不平衡回归问题上都超过了最好的现有方法。结合我们之前的工作Balanced Softmax，我们为不平衡分类与回归提供了一个统一的视角，希望更多的不平衡分类技巧可以借此引入不平衡回归问题中。

作者信息